 |
| MOVIE 1: 6 minutes 17 seconds |
|
Terminal Speed
Most anyone not schooled in classical physics would claim
that heavy things always fall faster than lighter things.
The NASA movie shows one of the Apollo astronauts demonstrating
from the surface of the moon the fall of a feather and
a heavy object dropped at the same time. They hit the
surface of the moon at the same moment. How can this happen?
Newton asked the opposite question: isn’t this what
you should expect, unless something interferes? Newton
realized that to make a clean description of how a body
moves, you have to imagine what it will do with no friction
or drag, and then put friction back into the picture as
a force like any other.
Air drag affects the picture in a special way because
it’s a force that increases with speed. This means
that for a given object falling through air, there will
be a speed at which its air drag (an upward force) is
as strong as its weight (which is pulling it downward).
Once it reaches this speed, so that these two forces cancel,
there will be no net force to accelerate it further, so
(by Newton’s first law) it continues at this speed,
which is called its terminal speed.
Things whose weight is small for their size, like feathers,
will have low terminal speeds -- they will not fall fast
in air because even at a low speed their air drag will
become strong enough to cancel their weight. This effect
creates the familiar experience that heavy things fall
faster.
The moon has no atmosphere and so air drag does not exist
there. On the moon, Newton's second Law of Motion
(click link to see earlier page for more information), rules
during the entire freefall of an object on the moon --
the body accelerates until it reaches the surface of the
moon. With the force due to the moon's gravity working
unimpeded, the feather and heavier object speed up at
the same rate. (One common question people have is why
a larger mass, which experiences a greater force of gravity,
does not speed up faster than a lighter object. The short
answer is that the greater mass' increased inertia offsets
the increased force of gravity, leaving the accelerations
of a lighter and heavier body equal.)
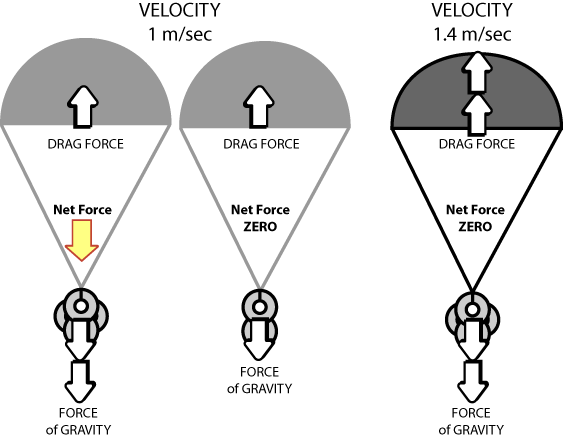
Look at the picture to the right. Suppose the two parachutes
are the same size but one has twice as heavy a load. When
the lighter and heavier loads fall, they start off accelerating
or increasing their speed downward because gravity's force
downward is greater than the drag force upward. At some
speed, let's say 1 m/sec, the drag force for this size
of chute equals to the force of gravity on the lighter
load and its parachute. The net force on this parachute
system then is zero, so this chute continues to travel
at the speed when it first had a net force of zero --
1 meter per second. At this speed the more heavily-loaded
parachute experiences the same drag, but that drag force
does not yet equal its greater force of gravity. It still
has a net force downward, and so it continues to increase
in speed. When it reaches a new speed, 1.4 m/sec, the
drag force equals the force of gravity and now the heavier
chute is at its own terminal speed.
|